Tenía que ser precisamente Hans Driesch, hombre bien templado en el análisis científico y luego converso a las puras especulaciones de la Filosofía, quien esgrimiese «el punto de vista lógico» contra los graves avances teoréticos de la Relatividad. Hora es de decir, sin embargo, decisivamente, en loa de Einstein, que su teoría ha sido la más fecunda impulsión que se conoce en el acontecer de los tiempos. Y esto prescindiendo en absoluto de su valor de verdad, conformándonos, en definitiva, con su valor de agitación. Porque, aun en caso, nada improbable, de que se llegue a demostrar la falsedad de la teoría, siempre quedará flameando con todo vigor el hecho de la insuficiencia de las concepciones clásicas debeladas.

Siempre ha sido, ciertamente, Hans Driesch un filósofo. Supo, en otro tiempo, fundamentar sus trabajos biológicos, articulándolos casi en un sistema. Es, como sabemos, el fundador de una escuela vitalista. Su Philosophie des Organischen (Leipzig, 1909) es justamente famosa. (Desde aquí, ahora, me atrevería a indicar a los directores de las ediciones de la Revista de Occidente se atreviesen a desviarse un poco de sus preferencias, exageradamente anecdóticas, para dar al público español traducciones de libros más fundamentales, por ejemplo, este de Hans Driesch que citamos.) El neoescolástico Maritain, introductor de Hans Driesch en Francia, decía, sin embargo, de este filósofo, creo que en 1912, que era aún «étranger aux études proprement méthaphysiques». Estrictamente podemos decir que era entonces un completo hombre de ciencia que ya amaba y comprendía la filosofía, pero que no hacía aún filosofía. Luego, posteriormente, ha derivado a estos campos con toda felicidad y éxito. Y en esta situación ha sido cuando se creyó en el deber de hacer una crítica lógica de la teoría de la Relatividad, de Einstein. Que vamos a analizar muy brevemente.

No es difícil, en realidad, combatir una teoría. Precisamente por ser discutible, es una teoría y no otra cosa, en el rango de los conocimientos. Pero una teoría es, ha de ser, cuando menos, lógica, y por eso no deja de ser extraño que en nombre del «punto de vista lógico» se la combata. Algo de esto ocurre en el empeño de Hans Driesch. ¿Quiere esto decir que se niegue a la Relatividad hasta el derecho de ser una teoría? Justamente esto se propone Hans Driesch hacer. En su análisis de la teoría especial o restringida de Einstein llega incluso a denunciar el hecho gravísimo de que se vulnera el principio de contradicción. Es casi de una extraña ingenuidad el denunciar un hecho así. No es creíble que los relativistas olvidasen de esa forma la esencia misma de su pensamiento. Todo gira alrededor de la dificultad que consiste en conceder a c (velocidad de la luz) una categoría de privilegio. Es un paso difícil para el lógico, pero que se vence, si nos fijamos en que se trata de introducir un concepto superior.

La Relatividad restringida, como todo el mundo sabe, consistió fundamentalmente en agrietar las concepciones de la Mecánica clásica, para atender a las exigencias de la Electrodinámica pujante. Esta había llegado a un desarrollo de tal forma contrario a las direcciones de la Mecánica vigente y, a la vez, de una manera tan firme y segura, que no había más remedio que considerarla como una monstruosidad, como un escándalo científico. Las tan traídas y llevadas ecuaciones de Lorentz son precisamente las ecuaciones fundamentales de la Electrodinámica. Einstein estableció su célebre principio partiendo de estas ecuaciones, presentándolas como las verdaderas ecuaciones de transformación de coordenadas referidas a sistemas legítimos. Las ecuaciones de Newton se obtienen de éstas sin hacer otra operación que ejecutar un paso al límite. Puede hablarse aquí de un afinamiento, de una más exacta interpretación matemática de los fenómenos. Así, Descartes refirió el índice de refracción a los senos de los ángulos de refracción y de incidencia, en vez de hacerlo a los ángulos, como erróneamente calculaban los sabios griegos. Esta diferencia, que es ínfima, tratándose de ángulos pequeños, por la casi igualdad del arco y del seno, alcanzaba gran importancia tratándose de ángulos mayores. Este error, ya previsto por los griegos, los desvaneció Descartes con sólo precisar más exactamente las relaciones.

Las críticas más acerbas de Hans Driesch a Einstein no son, sin embargo, las que opone al principio de la Relatividad restringida, sino las que opone a la teoría general. Realmente, aquí está el peligro mayor y la dificultad más inasequible. Si bien declaramos que se sale totalmente de la cuestión. La agilidad mental de este filósofo es tan sobremanera briosa, que, encuentre un enemigo donde lo encuentre, arremete contra él. Entre sus fobias intelectuales están, al parecer, la Geometrías no-euclídeas. A las pocas páginas de análisis, tropieza con ellas y escribe decidido: «Todo gira en torno a la introducción de los llamados conceptos espaciales metageométricos o no-euclidianos, en las consideraciones de la ciencia natural.» De esta forma, la crítica se convierte en una crítica de la metageometría, como él dice. A nuestro juicio, semejante actitud es inaceptable. Con el mismo derecho pudo haber negado el cálculo diferencial absoluto, que Einstein aprovechó genialmente en su teoría gravitatoria. (Véase el trabajo de Rey Pastor: Ciencia abstracta y Filosofía natural. ) Pero Hans Driesch, de la misma manera que nada dijo en su crítica de la teoría especial sobre la nueva noción de masa, originada por ella, elude ahora cuanto puede hablar de la gravitación. Vamos, pues, a seguirle en su labor antino-euclidana. En primer lugar, ese afán constante por negar validez a las nuevas geometrías, ni aun como instrumento de cálculo en la Física, revela, en verdad, una predisposición absurda contra ellas. Hoy, ya podemos afirmar que no hay geometrías más o menos ciertas, sino geometrías más o menos cómodas y aproximadas. Esto, por lo menos, se ve obligado a decir el físico. No es precisamente argumento eficaz el rechazar algunas de ellas a título de que no son intuitivas. Hay muchas cosas inintuibles, por ejemplo, las fuerzas magnéticas, para no salirnos del campo de la Física, y no por ello sería legítimo negarles realidad. Los trabajos de Gauss y otros geómetras no-euclidianos son irreprochables y conducen a magnas perspectivas. Yo me fijo ahora en unas fórmulas de Gauss, en que aparece una constante, k, que ocupa en ellas un lugar de auténtico privilegio. Véase, pues: Gauss llega a determinar, como longitud de la circunferencia de radio r,

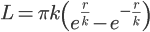
y añade que, para que esta fórmula esté de acuerdo con la experiencia, no hay sino suponer a k infinitamente grande. En efecto, basta sustituir cada exponencial por el desarrollo en serie y hacer k = ¥ para obtener la fórmula euclidiana L=2πr (Véase Vorlesungen über die Nicht-Euklidische Geometrie, de F. Klein, Gottinga, 1893, o la más elemental de Bonola, Geometrías no-euclidianas, traducción española, Madrid, 1923). Lobatschefski, el genial creador de la Pangeometría o Geometría imaginaria, llegó a resultados aún más interesantes. No podemos entrar aquí en su análisis. Baste señalar que siempre aparecen los cálculos euclidianos como simples casos particulares. Hay así también una constante, k, en sus fórmulas. Lobatschfski trata entonces de determinar el valor de esa constante. Valiéndose del paralaje de Sirio, que introduce en sus cálculos, concluye que el valor de k es, desde luego, enorme, respecto al diámetro de la Tierra. Y tomando paralajes menores, hasta 0’’1, resulta para k una cantidad enormísima. No extrañe, pues, que en la experiencia resulte válida y suficiente la hipótesis euclídea. Habla Hans Driesch de la imposibilidad de representar o, mejor, de «intuir las figuras no-euclidianas como tales». No opongamos a esto que es bien fácil, por otro lado, representar en el plano euclídeo la Geometría hiperbólica, por ejemplo. Todo el mundo sabe que es suficiente para ello la formación de un sistema —un diccionario— de definiciones. La imposibilidad que señala Hans Driesch no sería, en todo caso, fundamental. La verdad geométrica subsiste independientemente de toda representación. No puede asustarnos ya la exigencia abstracta que esto significa. En el fondo, la misma Geometría analítica bordea de continuo la abstracción pura. Y todas las direcciones no-euclidianas están nutridas, vitalizadas, por afanes abstractos.

Dígase, dígase ahora si Einstein cometió pecado de ligereza científica al fundamentar sus teorías en cálculos no-euclidianos. Nada puede deducirse de aquí en favor de una dogmatización de cuál sea la esencia geométrica del espacio físico, como erróneamente cree Hans Driesch. Einstein resuelve este pleito diciendo que no puede hablarse de espacio euclídeo ni no-euclídeo, sino que es dependiente de los estados de gravitación. La teoría de la gravitación, repetimos, es la esencial contribución de Einstein a la nueva física. Que es adonde Hans Driesch debió haber apuntado. La gravitación es la única fuerza que no necesita tener en cuenta la naturaleza física ni química de los cuerpos, y es, según Einstein, «el fundamento intrínseco de las relaciones métricas del espacio tiempo». Las ecuaciones diferenciales de los potenciales gravitatorios ɣμν, que son el gran resultado de la nueva teoría, se convierten en primera aproximación en las ecuaciones de la Mecánica clásica. Prescindiendo de las pruebas experimentales, todas ellas astronómicas, tiene la teoría de la Relatividad la prueba que suministran las matemáticas. Pero éste es, precisamente, su máximo pecado para Hans Driesch. Su crítica es una crítica de los métodos matemáticos. Nada más. Que no los cree suficientes para fundamentar una ciencia natural. El problema, como se ve, es antiguo. En Hans Driesch es, sin embargo, un resabio de aquellos sus tiempos de biólogo. No la moda del antimaternatismo. ¡Todavía!

R. Ledesma Ramos

(La Gaceta Literaria, n. 44, 15 - Octubre - 1928)